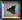Wave-Particle Duality Plus Heisenberg Uncertainty Principle Explains Single Slit Diffraction

In the above picture, the first equation is simple trigonometry. The second equation is the De Broglie equation for wave-particle duality connecting the wavelength to the momentum. The third equation is an application of the Heisenberg uncertainty principle since the vertical uncertainty in the particle's position is the width of the slit. The uncertainty principle then says that the vertical uncertainty (in the y direction) in the particle's momentum is Planck's constant (h) divided by the width (B) of the slit through which the particle passes.

The uncertainty in the scattering angle (delta theta) is approximately the vertical uncertainty (delta p sub y) in momentum divided by the horizontal momentum (p sub o) of the beam. Wave particle duality tells us that the horizontal momentum is Planck's constant over the horizontal wavelength of the beam. Putting it all together, Planck's constant cancels out, and we get the fourth equation which is the classical diffraction theory rule of thumb that the angular diffractive spread of the beam is well approximated by the horizontal wave length divided by the vertical width of the slit.

When the wave length is small compared to the slit width we have geometric optics in which light rays move along straight lines. The Schrodinger equation reduces to Newton's mechanics in an analogous limit where the wavelength of the particle is small compared to the regions over which there is significant variation in the potential energy of the particle.